Graph Embeddings in Neo4j
Table Of Contents
Introduction
What's an embedding
Graph Embedding
Graph Embeddings in Neo4j
Fast Random Projections (FastRP)
Node2Vec
GraphSAGE
Graph Embeddings for News Recommendation dataset
Introduction
Graph Embedding Algorithm 是 Neo4j 中的亮點。
這些算法用於將圖形的拓撲和特徵轉換為唯一表示每個節點的固定長度向量(或嵌入)。
Graph Embedding非常強大,因為它們保留了圖的關鍵特徵,同時以可解碼的方式降低了維數。 這意味著您可以捕獲圖形的複雜性和結構,並將其轉換為用於各種 ML 預測。
本文章將會簡單介紹Graph Embedding,並且實作Graph Embedding在Neo4j上(使用MIND News Dataset)
What's an embedding
- Google: "An embedding is a relatively low-dimensional space into which you can translate high-dimensional vectors"
- Wikipedia: "In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup.
我們可以把Embedding 想像成:一種將某物(文檔、圖像、圖表)映射到固定長度向量(或矩陣)的方法,該向量在降低維數的同時捕獲關鍵特性。
那我們如何embed人物呢?



你可以想像這是一隻小熊維尼,我們把這個小熊維尼用portrait的方式從三維空間轉換成二維度空間。這個Portrait embeds 小熊維尼到二維度空間表示。
但這個小熊維尼embedding有個非常重要的東西是他應該是一個簡化地表示,比最複雜的東西更簡單,但他依然應該是可識別的。
從上面三張embedding的圖,可以看到第一張圖太複雜了,有很多顏色,很多像素,很多訊息。而最右邊的那張可能又太簡化了。所以這是一個trade-off。
一幅肖像將一個三維人嵌入到二維空間中。
- 應該是一個簡化的表示,但是
- 表示仍應可識別
A portrait embeds a three-dimensional person into two-dimensional space.
- Should be a simplified representation, but
- The representation should still be recognizable
Graph Embedding
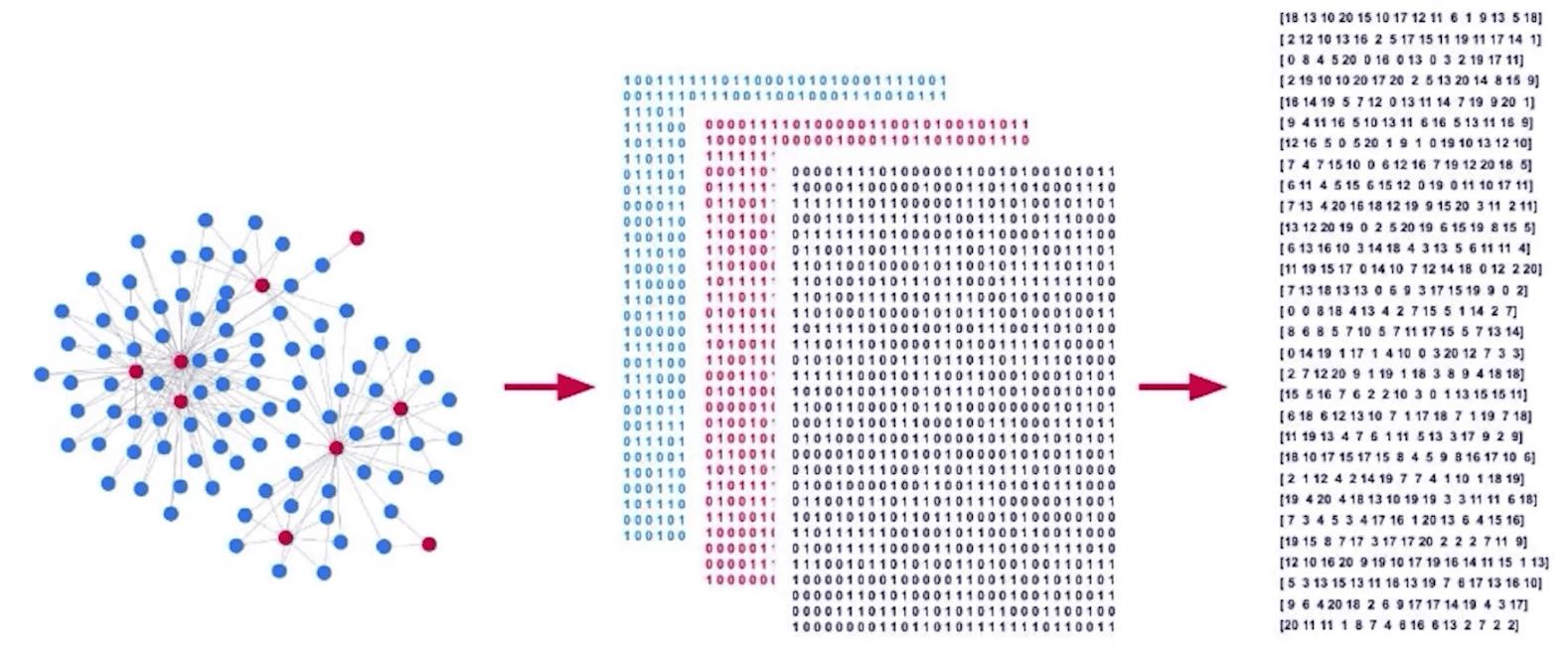
圖嵌入將你的圖轉換成固定長度的向量。
為了使其有用,我們的嵌入必須:保留關鍵特徵,降低維數,並進行解碼以重建你的圖。
A graph embedding translates your graph into fixed-length vectors.
To be useful your embedding must: preserve key features, reduce dimensionality, and may be decoded to reconstruct your graph.
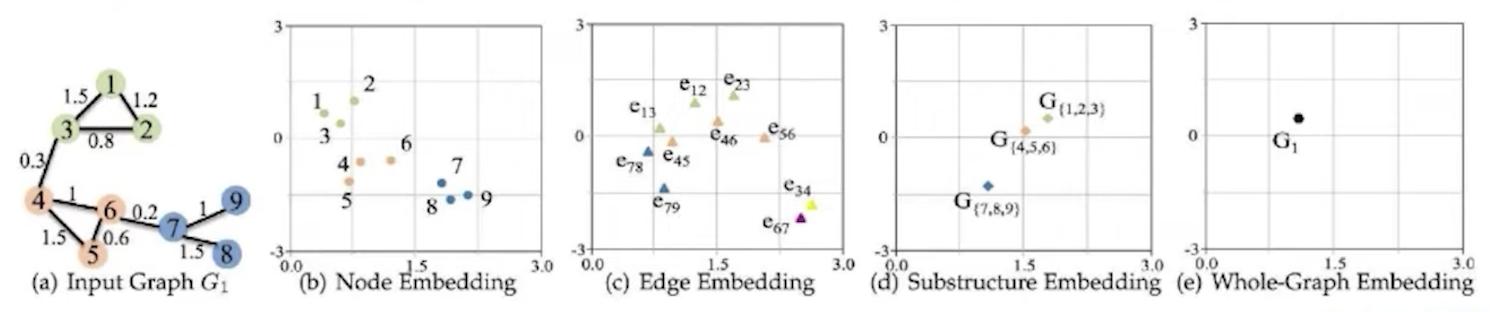
圖嵌入可以編碼圖的不同方面:
- 節點(頂點)嵌入: 描述每個節點的連通性
- 邊緣嵌入: 每個關係和它所連接的節點
- 路徑嵌入: 跨圖的遍歷
- 子圖嵌入: 編碼圖的一部分,像一個集群
- 圖嵌入: 將整個圖編碼為單個向量
Graph embeddings can encode different aspects of your graph:
- Node (vertex) embeddings: describe the connectivity of each node
- Edge embeddings: each relationship and the nodes it connects
- Path embeddings: traversals across the graph
- Subgraph embedding: encode a part of the graph, like a cluster
- Graph embeddings: encode an entire graph into a single vector
Why need a graph embedding?
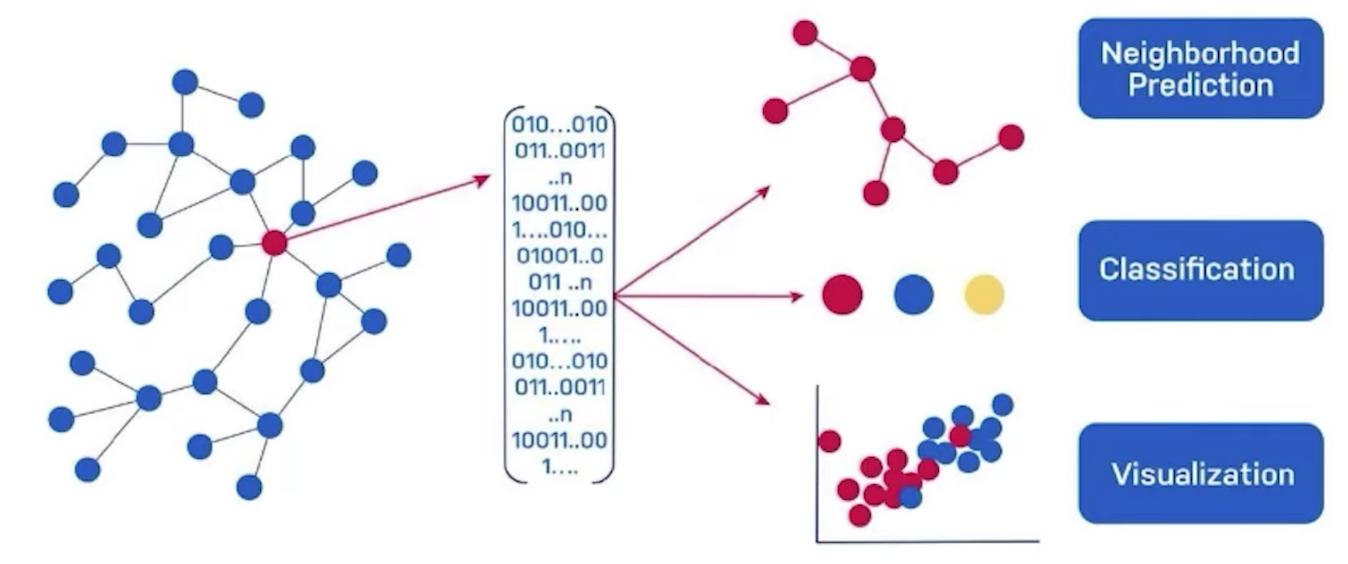
圖嵌入將您的圖轉換為有意義的數字,您可以將這些數字用作機器學習算法、簡化可視化或相似性度量的輸入。
Graph embeddings translate your graph into meaningful numbers that you can use as inputs for machine learning algorithms, simplified visualizations, or similarity measurements.
When to use graph embedding?
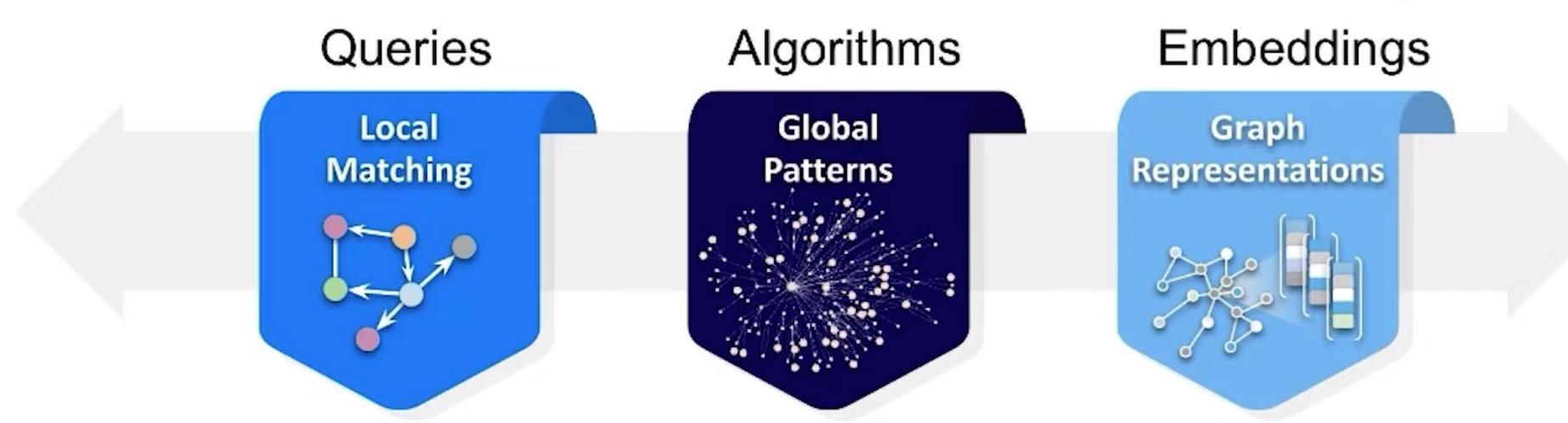
Intent Real-time local matching Find global patterns Create a highly predictive
for specific questions and trends for analytics numerical representation for
machine learning
Use When You know the exact pattern You know the kind of You know there's something
you're looking for patterns you're looking for important in the graph but
you don't know exactly what
to look for
Embeddings in Neo4j
Neo4j提供了三種類型的節點嵌入,可以將圖中的每個節點轉換為可靠的數字表示。
Neo4j offers three types of node embeddings, which can translate each node in your graph into a faithful numerical representation.
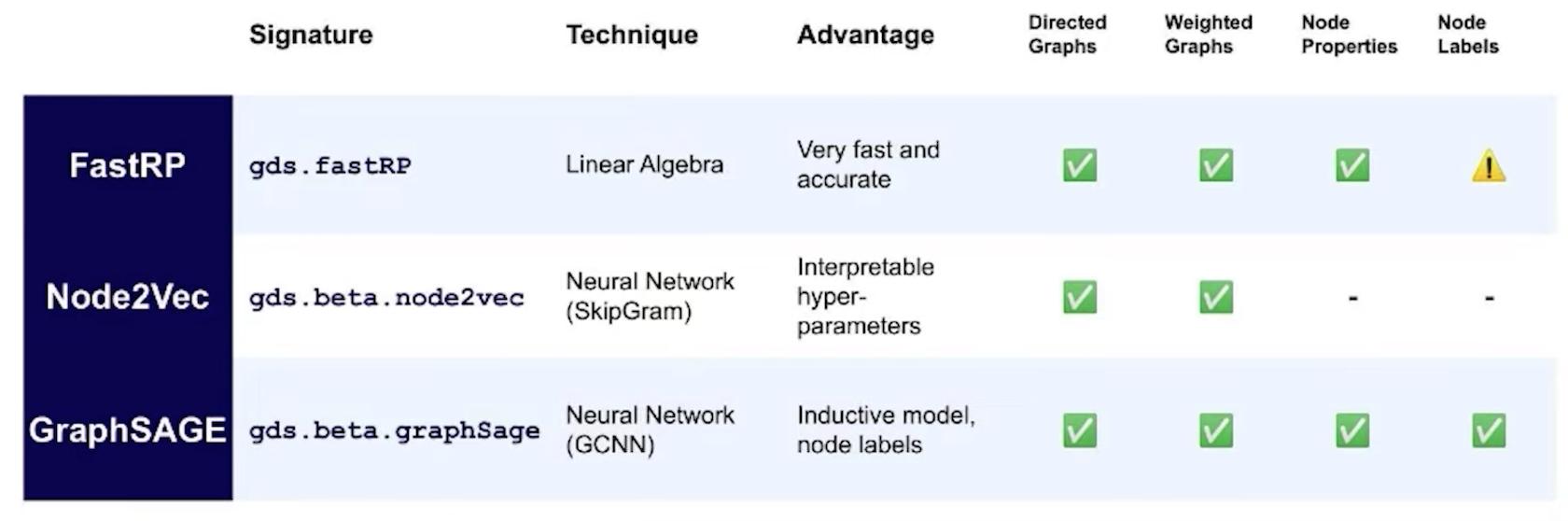
Fast Random Projections (FastRP)
Supported algorithm traits:
![]()
隨機投影嵌入使用稀疏隨機投影來生成嵌入。它是FastRP算法的一個實現。它是最快的嵌入算法,因此可以用來獲得baseline。它生成的嵌入通常與需要更長的運行時間的更複雜的算法具有同樣的性能。
FastRP通過基本線性代數實現 (Johnsson-Lindenstrauss Lemma)
The Random Projection embedding uses sparse random projections to generate embeddings. It is an implementation of the FastRP algorithm. It is the fastest of the embedding algorithms and can therefore be useful for obtaining baseline embeddings. The embeddings it generates are often equally performant as more complex algorithms that take longer to run.
FastRP works via basic linear algebra (Johnsson-Lindenstrauss Lemma)
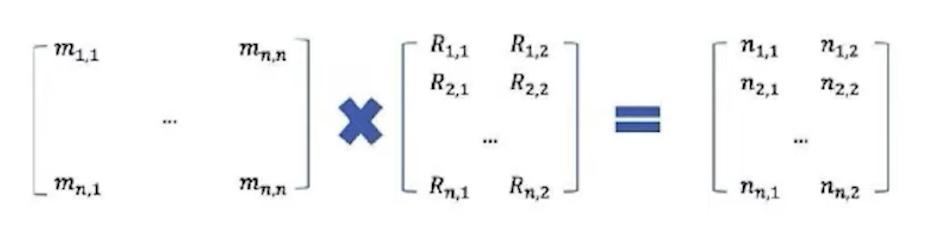
在每次迭代中,該算法通過平均上一個迭代或初始隨機向量的中間嵌入來構造中間嵌入。
At each iteration, the algorithm constructs an intermediate embedding by averaging the intermediate embeddings of neighbors from the last iteration or the initial random vector.
FastRP可以編碼節點屬性和權重
- 屬性由featureProperties指定,其影響由property Dimension確定。
- 節點嵌入是通過拓撲嵌入+屬性嵌入來構建的
- 屬性以與圖結構相同的方式嵌入:用一個隨機向量初始化節點屬性,然後在每次迭代中,平均相鄰節點的屬性。
FastRP can encode node properties and wights as well
- Properties are specified with featureProperties and their influence is determined with property Dimension.
- Node embedding are constructed by concatenating a topological embedding + a property embedding
- Properties are embedded in the same way as graph structure: node properties are initialized with a random vector, and then at each iteration, averaged across the properties of neighboring nodes.
Node2Vec
![]()
node2Vec基於節點鄰域的偏置隨機漫步計算嵌入。該算法訓練了一個單層前饋神經網絡,該網絡用於根據另一個節點的出現來預測一個節點在一次行走中出現的可能性。node2Vec具有一些參數,可以通過調整這些參數來控制隨機漫步的行為是更像廣度優先還是深度優先搜索。這種調整允許嵌入捕獲同質性(類似的嵌入捕獲網絡社區)或結構等效性(類似的嵌入捕獲節點的類似結構角色)。
Node2Vec借用了word embedding技術: 使用隨機漫步採樣上下文windows,並訓練skipgram模型。
node2Vec computes embeddings based on biased random walks of a node’s neighborhood. The algorithm trains a single-layer feedforward neural network, which is used to predict the likelihood that a node will occur in a walk based on the occurrence of another node. node2Vec has parameters that can be tuned to control whether the random walks behave more like breadth first or depth first searches. This tuning allows the embedding to either capture homophily (similar embeddings capture network communities) or structural equivalence (similar embeddings capture similar structural roles of nodes).
Node2Vec borrows from word embedding techniques: using random walks to sample context windows, and training a skipgram model.
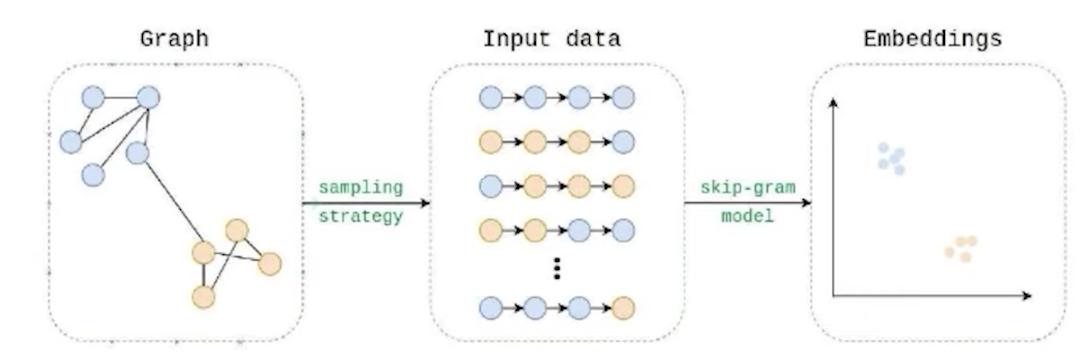
Node2Vec很酷,因為它可以學習同質性(相鄰節點)或結構性嵌入。
Node2Vec is cool because it can learn either homophily (neighboring node) or structural embeddings.
GraphSAGE
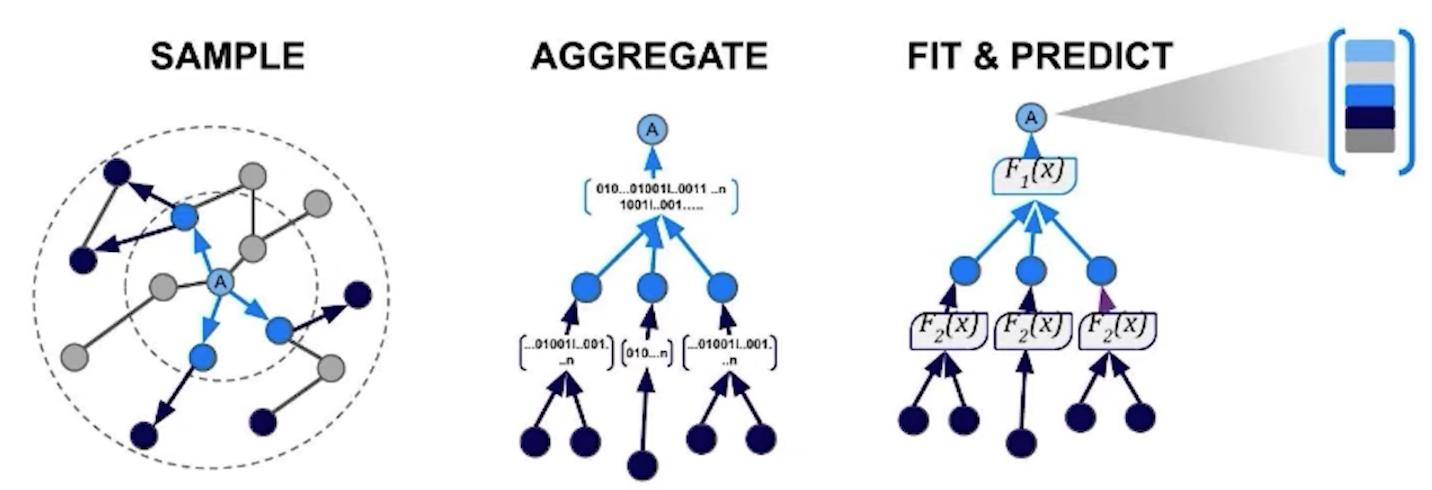
GraphSAGE 是唯一支持節點屬性的算法。包含節點屬性的訓練嵌入對於包含圖拓撲之外的信息(如元數據、屬性或其他圖算法的結果)很有用。GraphSAGE與其他算法的不同之處在於,它學習一個函數來計算嵌入,而不是訓練每個節點的單個嵌入。
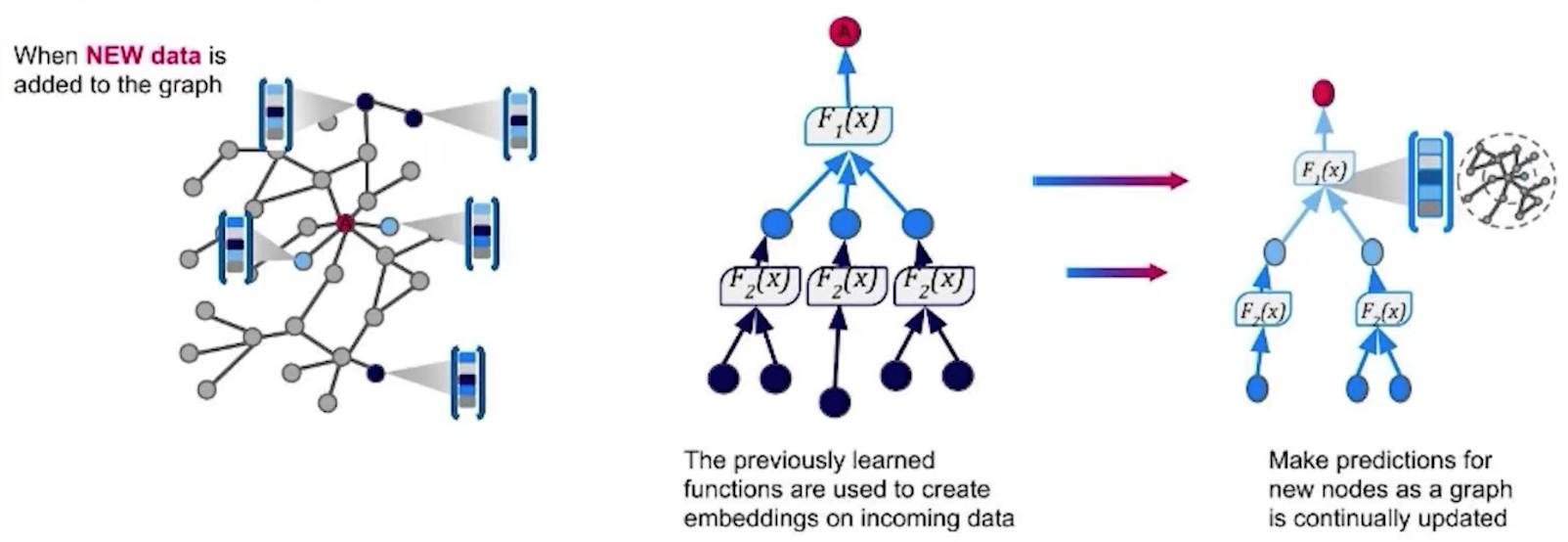
GraphSAGE學習節點及其屬性的表示,並返回一個歸納模型:這意味著您可以為以前未見的新數據生成嵌入。
GraphSAGE is the only one that supports node properties. Training embeddings that include node properties can be useful for including information beyond the topology of the graph, like meta data, attributes, or the results of other graph algorithms. GraphSAGE differs from the other algorithms in that it learns a function to calculate an embedding rather than training individual embeddings for each node.
GraphSAGE learns representations of nodes and their properties and returns an inductive model: this means you can generate embeddings for new, previously unseen data.
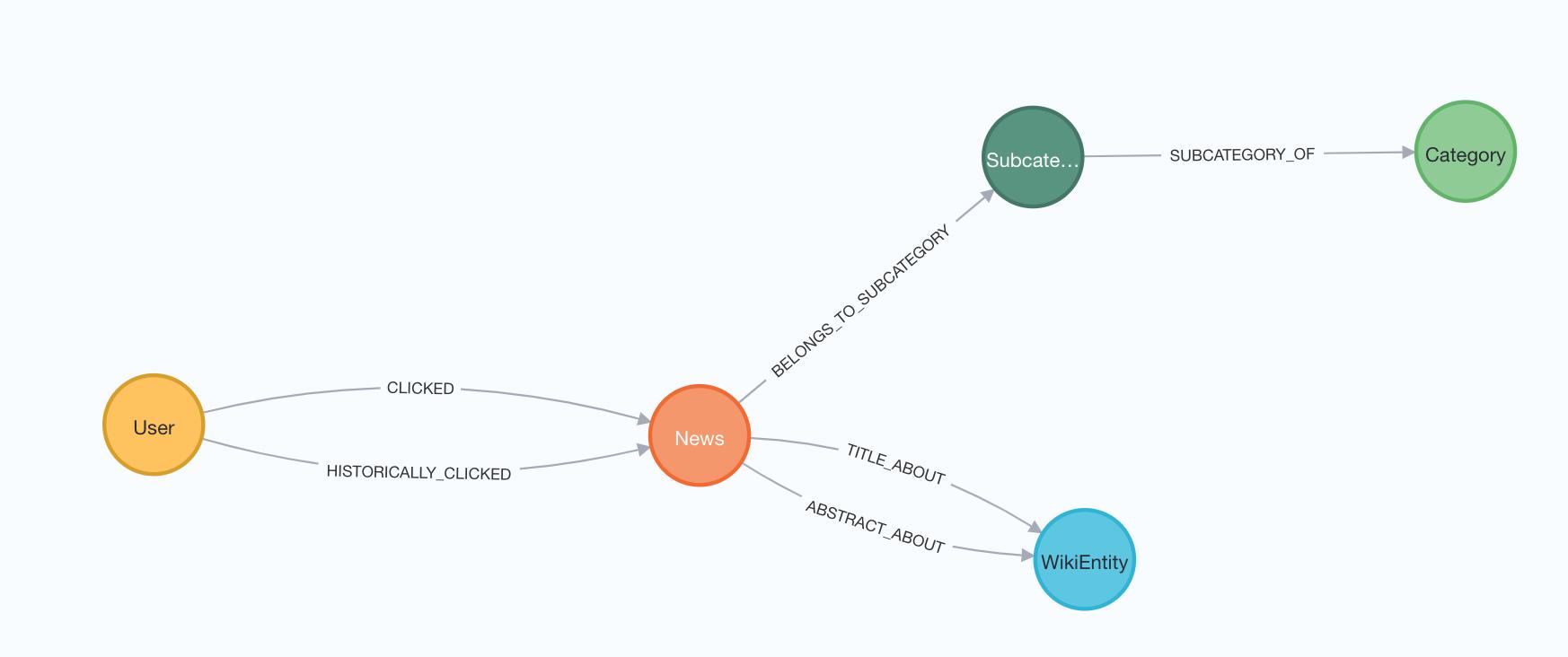
Graph Embeddings for News Recommendations Dataset
Data Set:
Almost 100k users and their MSN news click behaviors. Made publically available by Microsoft.
Prerequisites:
- Neo4j: 4.4.0
- APOC library: 4.4.0
- Graph Data Science (GDS) Library = 1.8.0
FastRP:
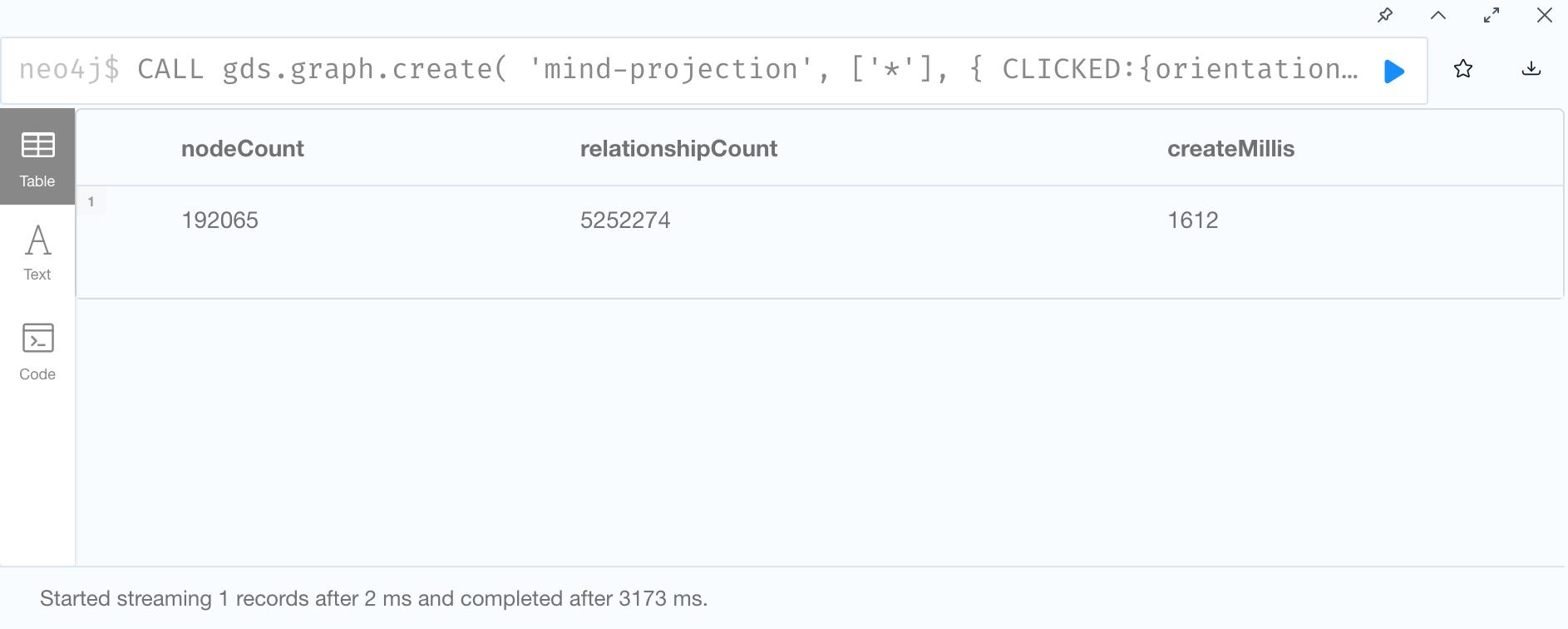
1. Create Graph Projection
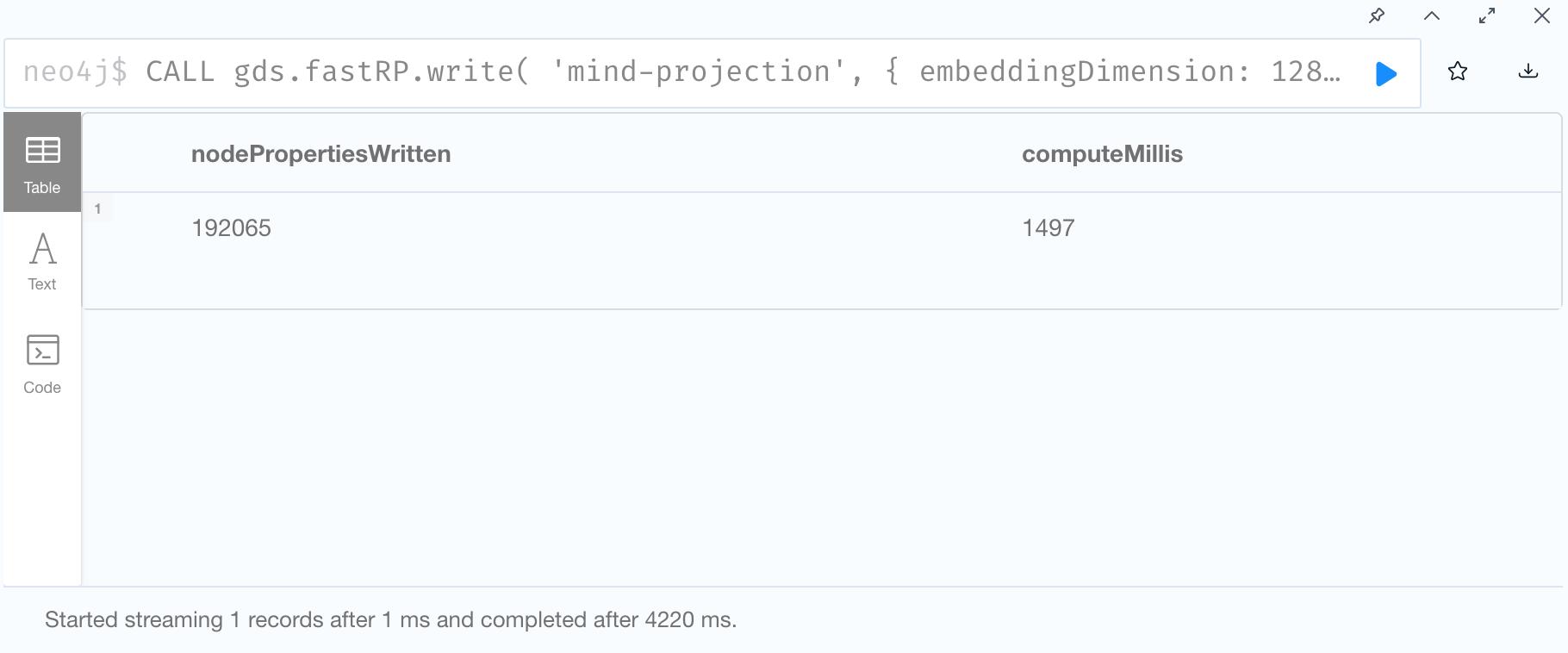
2. Run FastRP and Write back to graph database
3. See the FastRP result
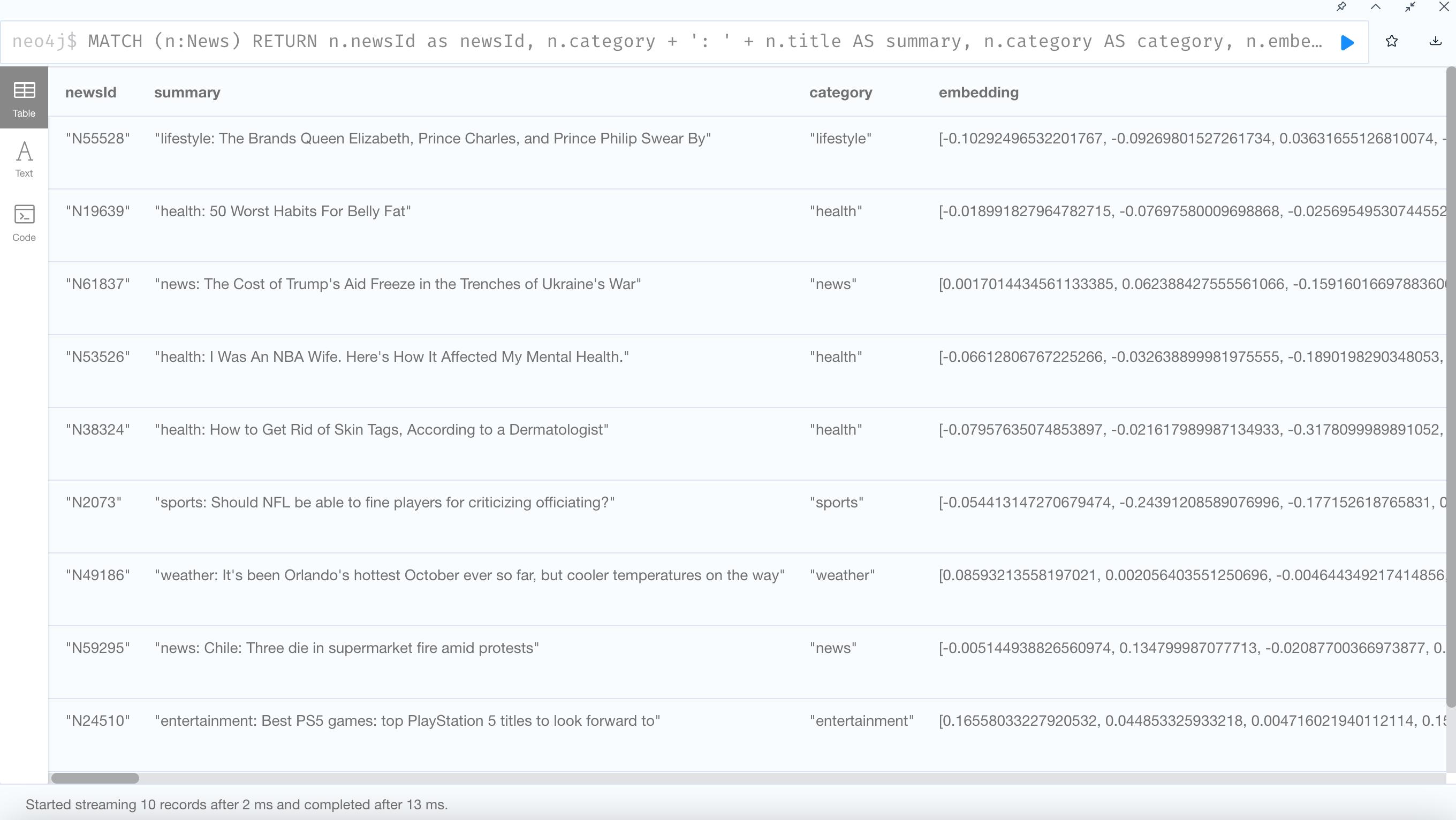
Node2Vec:
1. Create Graph Projection
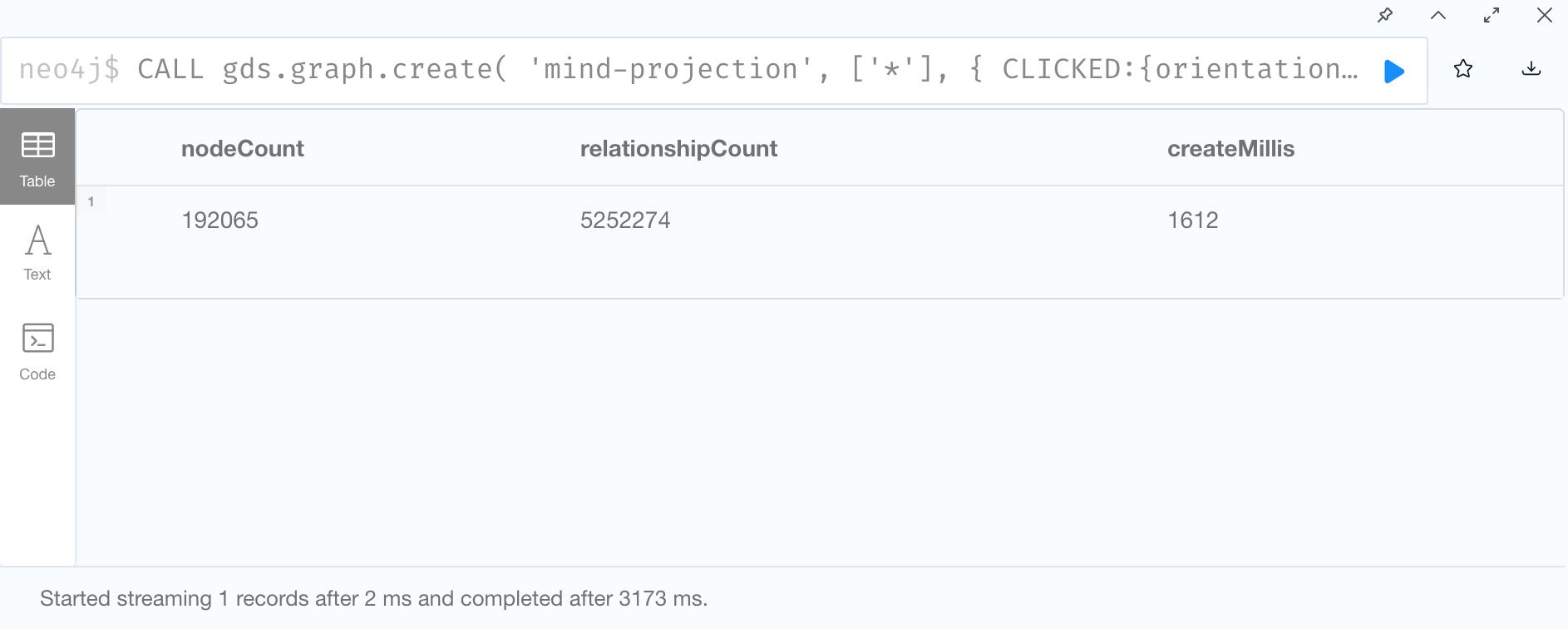
2. Node2Vec Embedding and Write back to graph database
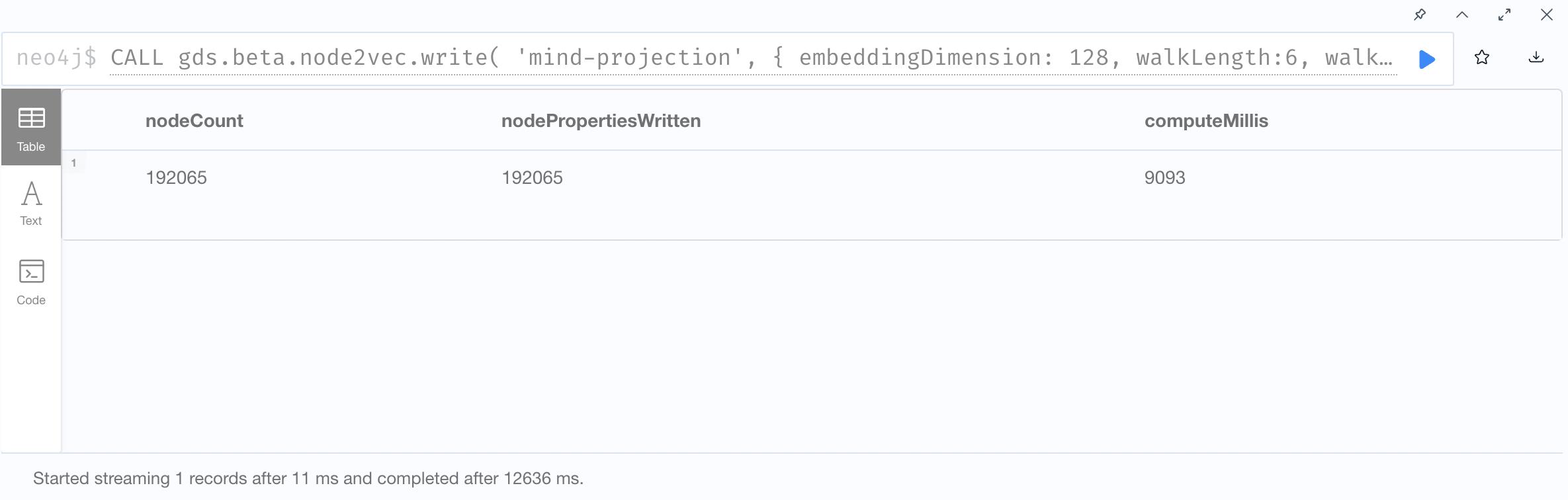
3. Show results
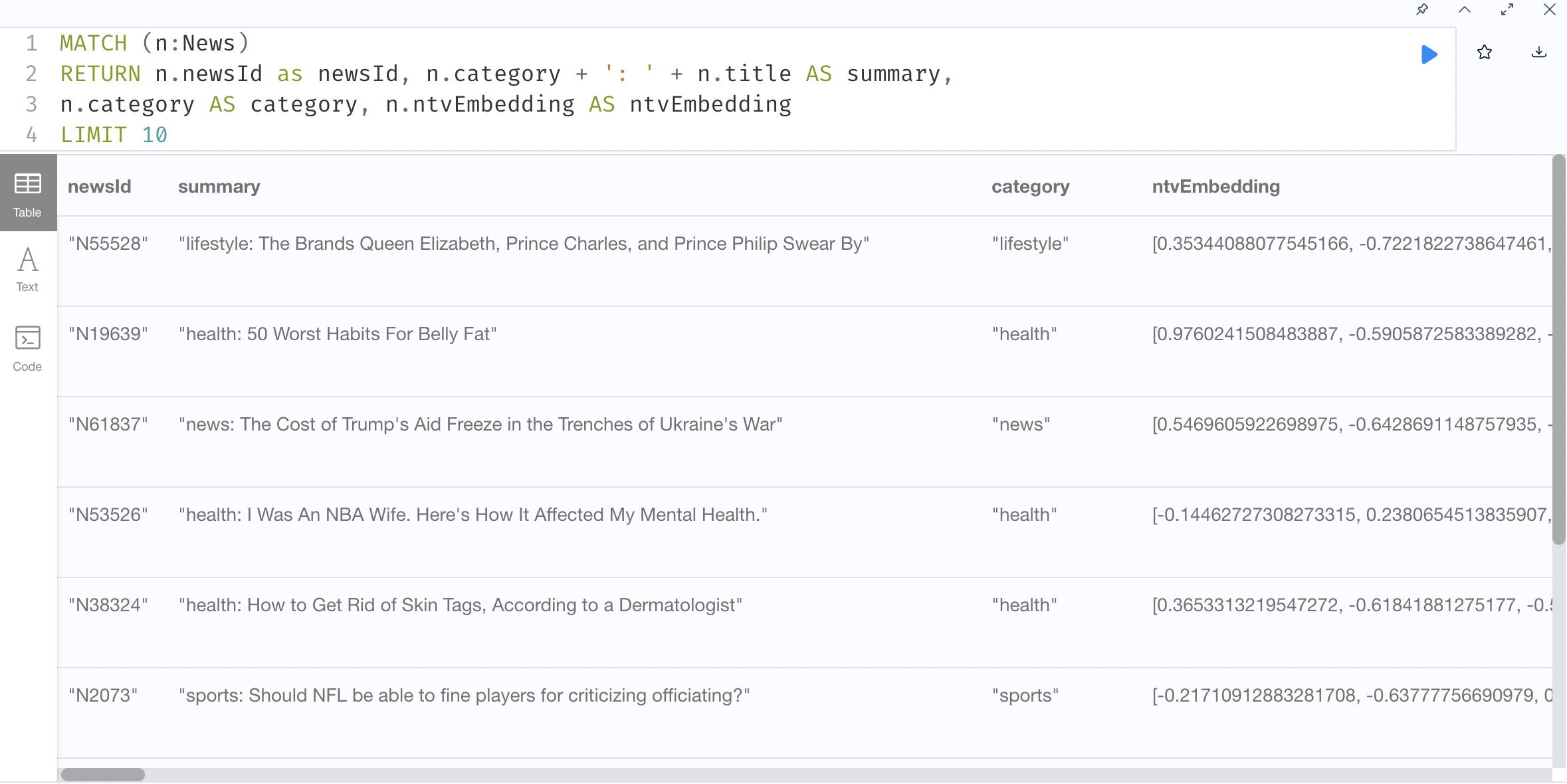
GraphSAGE:
1. Create Graph Projection
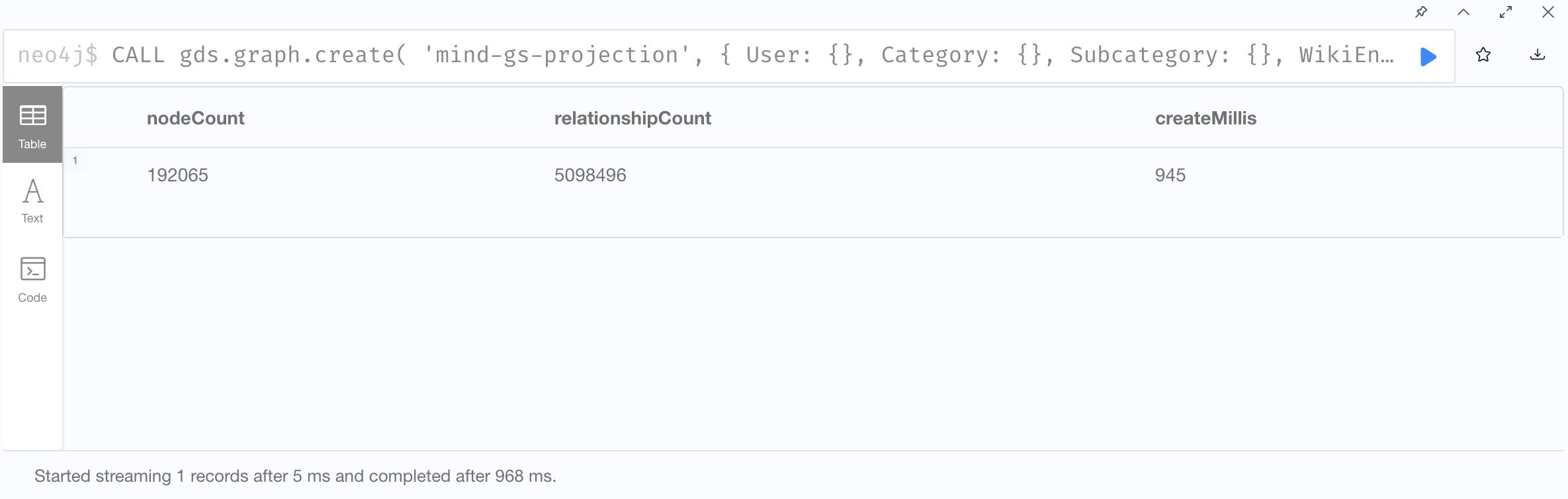
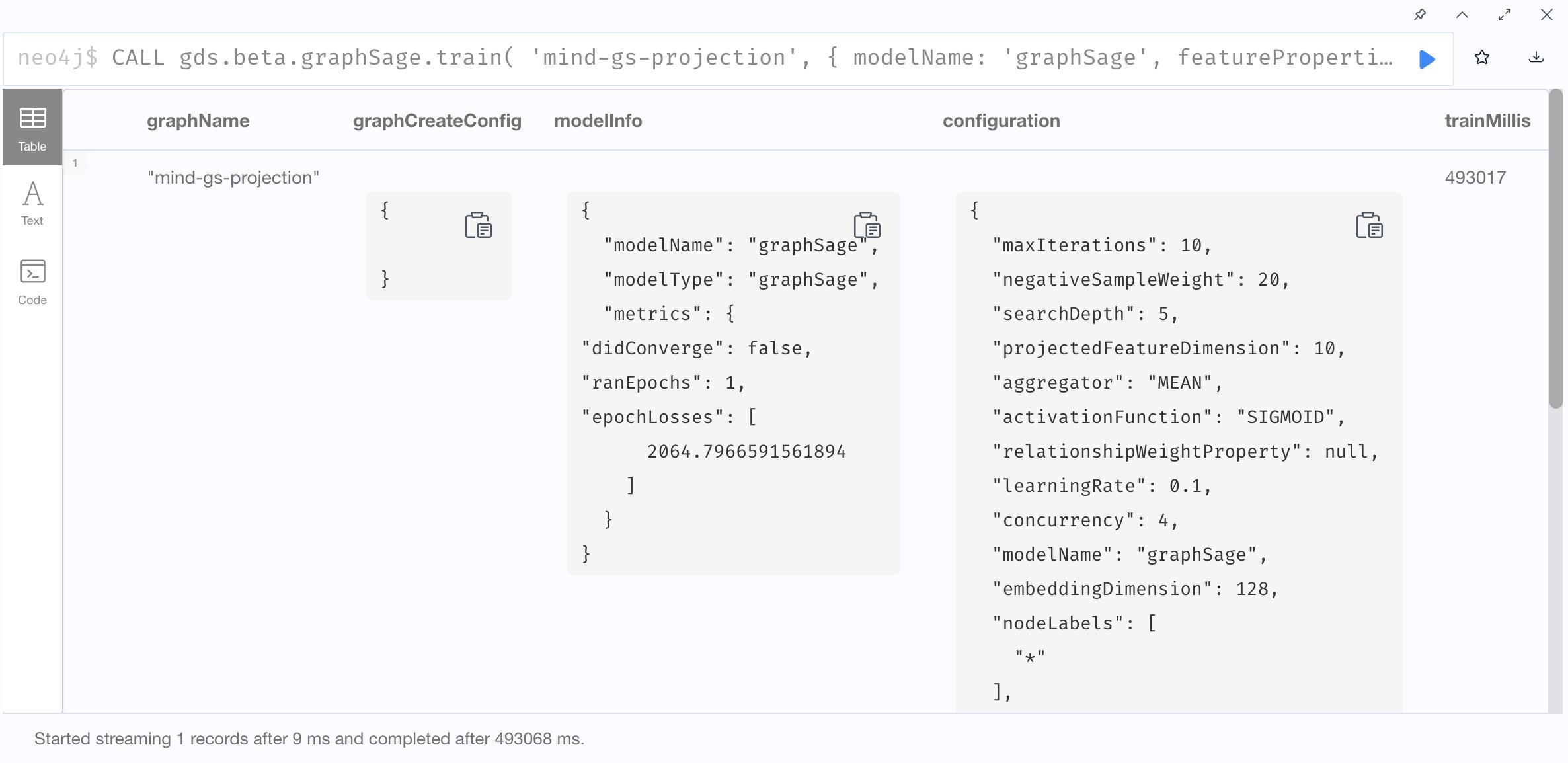
2. Train GraphSage
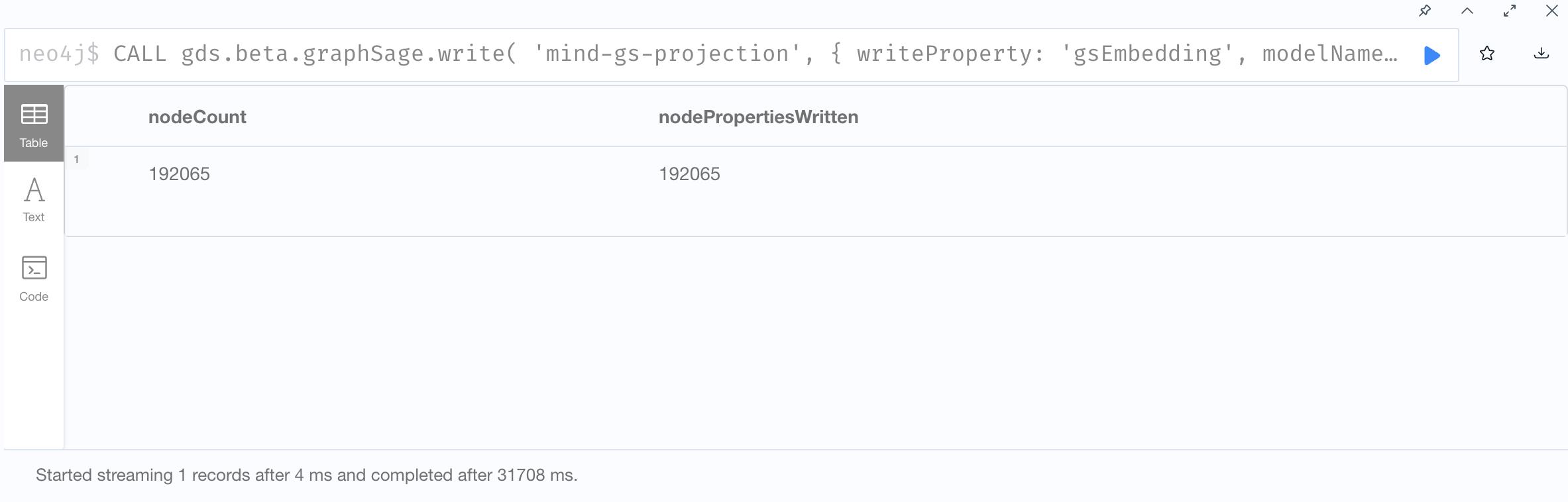
3. Write graphSage embeddings
4. Show results